Circumference of the smaller circle, using
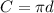
, is approximately equal to 18.85 (I used the high floating point precision approximation of pi my calculator has in memory, then rounded to 2 decimal points.)
Using the formula
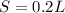
, which in English says "the smaller circle's circumference is equal to 20% of the larger circle's", we can substitute the known value S:
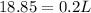
and solve for L:
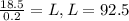
.
So the larger circle has a circumference approximately equal to 92.5 units.