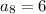Question

Write a explicit formula for the sequence 10, 9.5, 9, 8.5, 8 then find ^a8

Answer 1

The term number eight is 6.5

`a_(8)=6.5`

Explanation:

The given sequence is an arithmetic sequence, because each term can be found by applying a difference.

In this case, you can observe that such difference is -0.5, because each term is going down by 0.5 units.

The formula that describes an arithmetic sequence is

`a_(n)=a_(1)+(n-1)d`

Where
`a_(n)` is the last term,
`a_(1)` is the first term,
`n` is the position of the last term and
`d` is the difference.

Each variable is

`a_(1) =10\\d=-0.5\\n=8\\`

Where we are gonna find
`a_(8)` the term number eight. So, replacing values, we have

`a_(n)=a_(1)+(n-1)d\\a_(8)=10+(8-1)(-0.5)\\a_(8)=10+7(-0.5)=10-3.5\\a_(8)=6.5`

Therefore, the term number eight is 6.5.

Answer 2

Explicit formula for the sequence is
`a_n=10.5-0.5n` and
`a_8=6`

Explanation:

Given: Sequence = 10, 9.5 , 9 , 8.5 , 8

To find: Explicit Formula for the sequence and 8th term of sequence

1st term of sequence = 10

2nd term of sequence = 9.5

3rd term of sequence = 9

4th term of sequence = 8.5

5th term of sequence = 8

Difference between 2nd and 1st term = 9.5 - 10 = -0.5

Difference between 3rd and 2nd term = 9 - 9.5 = -0.5

Since, Difference is same in both cases

⇒ It is Arthematic Progression

⇒ First term, a = 10 and Common term, d = -0.5

using formula of AP for nth term we get,

`a_n=a+(n-1)d`

`a_n=10+(n-1)(-0.5)`

`a_n=10-0.5n+0.5`

`a_n=10.5-0.5n`

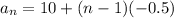
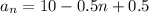
⇒ 8th Term of AP,
`a_8=10.5-0.5*8=10-4=6`

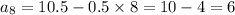
Therefore, Explicit formula for the sequence is
`a_n=10.5-0.5n` and
`a_8=6`