Question

The width and the length of a rectangle are consecutive even integers. If the width is decreased by 3 inches, then the area of the resulting rectangle is 24 square inches. What is the area of the original rectangle?

12 square inches
48 square inches
96 square inches

Answer 1

Credit from the first person. The Answer is 48^2 inches

Explanation:

Answer 2

Greetings!

To solve this problem, we will have to create a linear system:

Let Statements:
Let x represent the width of the first rectangle
Let y represent the length of the first rectangle

Linear System:
We can create the two equations (a system) using the information from the problem:

`\left \{ {{x+2=y} \atop {(x-3)(y)=24}} \right.`

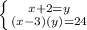
Solve the system using Elimination or Substitution.

Isolate for x, in Equation #1:

`x+2=y`


`x=y-2`

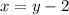Substitute this value into Equation #2:

`(x-3)(y)=24`


`((y-2)-3)(y)=24`

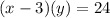
Simplify the Equation:

`(y-2-3)(y)=24`


`(y-5)(y)=24`

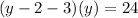
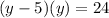Distribute the Parenthesis:

`(((y)(y))-(5)(y))=24`


`y^2-5y=24`

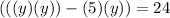
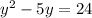Add -24 to both sides:

`(y^2-5y)+(-24)=(24)+(-24)`


`y^2-5y-24=0`

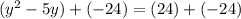
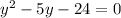
Factor the Simple Trinomial:

`y^2-8y+3y-24=0`


`y(y-8)+3(y-8)=0`


`(y-8)(y+3)=0`

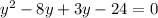
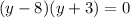Set Factors to equal 0:

First Factor: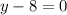

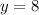`y-8=0`


`y=8`

Second Factor: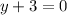

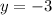
`y+3=0`


`y=-3`

Since it is impossible to have a "negative length" the only possible answer would be:

`\boxed{y=8}`

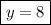
Using this value, find the value of x:

`x+2=y`


`x+2=(8)`

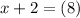
Add -2 to both sides:

`(x+2)+(-2)=(8)+(-2)`


`\boxed{x=6}`

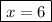
To find the area of the first rectangle, we can use a formula:

`A_(Rectangle)=(l)(w)`

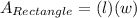Input the values:

`A_(Rectangle)=(8)(6)`

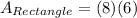Simplify:

`A_(Rectangle)=48`

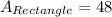The Area of the First Rectangle is:

`\boxed{=48in^2}`

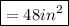
I hope this helped!
-Benjamin