Question

∠AED is formed inside a circle by two intersecting chords. If minor arc BD = 82 and minor arc CA = 176, what is the measure of ∠ AED?

Answer 1

∠BED=1/2 (arc AC+arc BD)
∠BED=1/2 (176+82)
∠BED=1/2 (258)
∠BED= 129

∠AED=180-129=51

Answer 2

Answer: The measure of ∠AED = 51°.

Explanation:

Since we have given that

∠AED is formed inside a circle by two intersecting chords.

Measure of minor arc BD = 82

and Measure of minor arc CA = 176

So, We know that the measure of the angle is equal to half of the sum of measure of two arcs intercepted by the angle and its respective vertical angle.

As shown in the figure.

We will get the measure of the angle ∠BED, according to the given arcs.

So, it becomes,

`\angle BED=(BD+AC)/(2)\\\\\angle BED=(82+176)/(2)\\\\\angle BED=129^\circ`

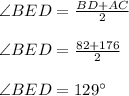
Since ∠ AED formed linear pair with ∠BED.

So, the measure of ∠ AED is
`180^\circ-129^\circ=51^\circ`