Question

questionSuppose $24,000 is deposited into an account paying 7.25% interest, which is compoundedcontinuouslyHow much money will be in the account after ten years if no withdrawals or additional depositsare made?

Answer 1

This is a compound interest question and we have been given:

Principal (P) = $24000

Rate (r) = 7.25%

Years (t) = 10

However, we are told this value is compounded continuously. This means that for every infinitesimal time period, the value keeps being compounded.

The formula for finding the compound interest is:

`\text{Amount}=P(1+(r)/(n))^(nt)`

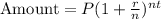
But because the compounding period is continuous and therefore, infinitesimal,

`\begin{gathered} Amount=P(1+(r)/(n))^(nt) \\ But, \\ n\to\infty \\ \\ \therefore Amount=\lim _(n\to\infty)P(1+(r)/(n))^(nt) \end{gathered}`

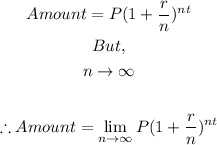
This is similar to the general formula for Euler's number (e) which is:

`e=\lim _(n\to\infty)(1+(1)/(n))^n`

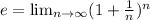
Thus, we can re-write the Amount formula in terms of e:

`\begin{gathered} \text{Amount}=\lim _(n\to\infty)P(1+(r)/(n))^(nt) \\ \text{This can be re-written as:} \\ \\ Amount=\lim _(n\to\infty)P(1+(r)/(n))^{(n)/(r)* r* t}\text{ (move P out of the limit because it is a constant)} \\ \\ \text{Amount}=P\lim _(n\to\infty)((1+(r)/(n))^{(n)/(r)})^(r* t) \\ \\ \text{Amount}=P(\lim _(n\to\infty)(1+(r)/(n))^{(n)/(5)})^(rt) \\ \\ \text{but,} \\ e=(\lim _(n\to\infty)(1+(r)/(n))^{(n)/(r)} \\ \\ \therefore\text{Amount}=Pe^(rt) \end{gathered}`

Therefore, we can find the amount of money in the account after 10 years:

`\begin{gathered} \text{Amount}=Pe^(rt) \\ P=24000 \\ r=7.25\text{ \%=}(7.25)/(100)=0.0725 \\ t=10\text{ years} \\ \\ \therefore\text{Amount}=24000* e^(10*0.0725) \\ \\ \text{Amount}=24000*2.06473 \\ \\ \therefore\text{Amount}=49553.546\approx49553.55 \end{gathered}`

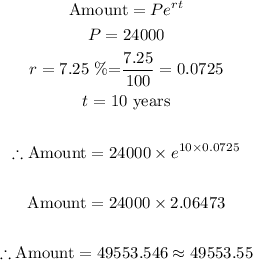
Therefore the amount after compounding continuously for 10 years is:

$49553.55