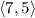We will have the following:
2)
A(0, 7) : <7, -3>
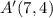
B(1, 3) : <7, -3>

C(-1, -4) : <7, -3>
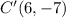
D(-5, 1) : <7, -3>
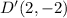
3)
From the graph we will have the following:
a.
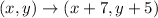
b.
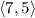
***Explanation***
For point 2, we will simply apply the vector to the corresponding coordinates, that is:
We have the coordinates:
and the vector:
So, in order to determine the final image we will have to follow the transformation rule:
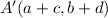
*For point 3, we will simply count the number of units the image has moved to the left or rigth and that will be our transformation rule for the x-axis, and the number of units the image has moved up or down and that will be our transformation rule for the y-axis.
In the case of the problem, the images moved 7 units to the rigth (+7) and then moved 5 units up (+5), so the transformation rule in coordinate notation is given by:
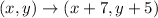
And in order to write it in vector notation, we simply write the units the images move: