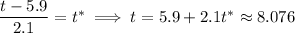Question

the patient recovery time from a particular surgical procedure is normally distributed with a mean of 5.9 days and a standard deviation of 2.1 days. What is the 85th percentile for recovery times?

Answer 1

The 85th percentile is the cutoff time
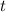
`t` such that


`\mathbb P(X<t)=0.85`

In other words, the 85th percentile refers to the time needed to belong to the top 15% of the distribution; more generally, the
`n` percentile is the top
`(100-n)\%` of the distribution.

Anyway, to find this value of
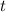
`t`, transform
`X` to a random variable
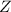
`Z` with the standard normal distribution using


`Z=\frac{X-\mu}\sigma`

where
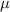
`\mu` is the mean of
`X` and
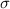
`\sigma` is the standard deviation of
`X`.


`\mathbb P(X<t)=\mathbb P\left((X-5.9)/(2.1)<(t-5.9)/(2.1)\right)=\mathbb P(Z<t^*)=0.85`

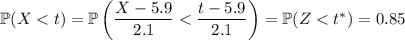
Here
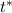
`t^*` is used to denote the z-score corresponding to the cutoff time
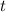
`t`. Referring to a z-score table, you find that this occurs for
`t^*\approx1.036`. So,


`(t-5.9)/(2.1)=t^*\implies t=5.9+2.1t^*\approx8.076`