Answer:
x = -1/7, y = 6/7
System:
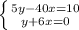
Explanation:
The system of equations would be
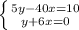 .
.
To find out what x and y are, choose one of the equation and solve for y. Then, substitute the result for y into the other equation.
5y - 40x = 10 (Add 40x to both sides)
5y = 40x + 10 (Divide both sides by 5)
y = 1/5(40x + 10) (Multiply 40x + 10 by 1/5)
y = 8x + 2 (Substitute this for y in the other equation.)
8x + 2 + 6x = 0 (Add 8x to 6x)
14x + 2 = 0 (Subtract 2 from both sides)
14x = -2 (Divide both sides by 14)
x = -1/7 (Substitute this for x in the y = 8x + 2)
y = 8(-1/7) + 2 (Multiply -1/7 by 8)
y = -8/7 + 2 (Convert 2 into 14/7; show as a single fraction)
y = (-8 + 14)/7 (Add -8 and 14)
y = 6/7 (The system is solved)