Question

Can someone please help me on number 16-ABC

Answer 1

Please check the explanation.

Explanation:

Given the inequality

-2x < 10

-6 < -2x

Part a) Is x = 0 a solution to both inequalities

FOR -2x < 10

substituting x = 0 in -2x < 10

-2x < 10

-3(0) < 10

0 < 10

TRUE!

Thus, x = 0 satisfies the inequality -2x < 10.

∴ x = 0 is the solution to the inequality -2x < 10.

FOR -6 < -2x

substituting x = 0 in -6 < -2x

-6 < -2x

-6 < -2(0)

-6 < 0

TRUE!

Thus, x = 0 satisfies the inequality -6 < -2x

∴ x = 0 is the solution to the inequality -6 < -2x

Conclusion:

x = 0 is a solution to both inequalites.

Part b) Is x = 4 a solution to both inequalities

FOR -2x < 10

substituting x = 4 in -2x < 10

-2x < 10

-3(4) < 10

-12 < 10

TRUE!

Thus, x = 4 satisfies the inequality -2x < 10.

∴ x = 4 is the solution to the inequality -2x < 10.

FOR -6 < -2x

substituting x = 4 in -6 < -2x

-6 < -2x

-6 < -2(4)

-6 < -8

FALSE!

Thus, x = 4 does not satisfiy the inequality -6 < -2x

∴ x = 4 is the NOT a solution to the inequality -6 < -2x.

Conclusion:

x = 4 is NOT a solution to both inequalites.

Part c) Find another value of x that is a solution to both inequalities.

solving -2x < 10

`-2x\:<\:10`

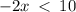
Multiply both sides by -1 (reverses the inequality)

`\left(-2x\right)\left(-1\right)>10\left(-1\right)`

Simplify

`2x>-10`

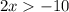
Divide both sides by 2

`(2x)/(2)>(-10)/(2)`

`x>-5`

`-2x<10\quad :\quad \begin{bmatrix}\mathrm{Solution:}\:&\:x>-5\:\\ \:\mathrm{Interval\:Notation:}&\:\left(-5,\:\infty \:\right)\end{bmatrix}`

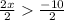
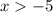
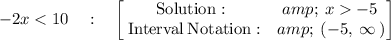
solving -6 < -2x

-6 < -2x

switch sides

`-2x>-6`

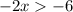
Multiply both sides by -1 (reverses the inequality)

`\left(-2x\right)\left(-1\right)<\left(-6\right)\left(-1\right)`

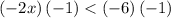
Simplify

`2x<6`

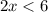
Divide both sides by 2

`(2x)/(2)<(6)/(2)`

`x<3`

`-6<-2x\quad :\quad \begin{bmatrix}\mathrm{Solution:}\:&\:x<3\:\\ \:\mathrm{Interval\:Notation:}&\:\left(-\infty \:,\:3\right)\end{bmatrix}`

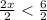
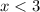
Thus, the two intervals:

`\left(-\infty \:,\:3\right)`

`\left(-5,\:\infty \:\right)`

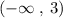
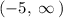
The intersection of these two intervals would be the solution to both inequalities.

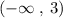`\left(-\infty \:,\:3\right)` and
`\left(-5,\:\infty \:\right)`

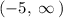
As x = 1 is included in both intervals.

so x = 1 would be another solution common to both inequalities.

SUBSTITUTING x = 1

FOR -2x < 10

substituting x = 1 in -2x < 10

-2x < 10

-3(1) < 10

-3 < 10

TRUE!

Thus, x = 1 satisfies the inequality -2x < 10.

∴ x = 1 is the solution to the inequality -2x < 10.

FOR -6 < -2x

substituting x = 1 in -6 < -2x

-6 < -2x

-6 < -2(1)

-6 < -2

TRUE!

Thus, x = 1 satisfies the inequality -6 < -2x

∴ x = 1 is the solution to the inequality -6 < -2x.

Conclusion:

x = 1 is a solution common to both inequalites.