Answer:
The general equation of parabola is given by:
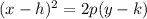 ....[1]
....[1]
where,
vertex = (h, k)
Focus = (0, p/2)
directrix : y = -p/2
and
p represents the focal width
Given the parabola:
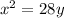
On comparing with [1] we have;
h=k =0
Vertex=(0, 0)
and
2p = 28
Divide both sides by 2 we have;
p = 14
Focus = (0, 14/2)
⇒Focus= (0, 7)
Directrix:
y = -14/2
⇒y = -7
Therefore, the equation of parabola
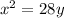 has
has
vertex = (0, 0)
focus = (0, 7)
directrix: y = -7
Focal width = 14