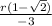Answer:
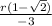
Explanation:
Volume of cone =
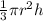
Since we are given that a circular cone has a base of radius r and a height of h that is the same length as the radius
=
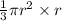
=
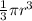
Surface area of cone including 1 base =
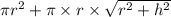
Since r = h
So, area =
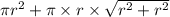
=
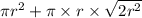
=
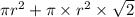
Ratio of volume of cone to its surface area including base :
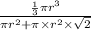
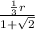
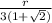
Rationalizing
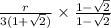
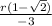
Hence the ratio the ratio of the volume of the candle to its surface area(including the base) is