Question

The length of a rectangle is 6 inches longer than its width. what are the possible widths if the area of the rectangle is at least 667 square inches

Answer 1

area=l×w
l=w+6
667=w(w+6)
w²+6w-667=0
w=23 or -29
w=23 only because distance cannot be negative

Answer 2

width must be atleast 23 inches.

Explanation:

Given that the length of a rectangle is 6 inches longer than its width.

If l is length, then w = l-6

Area =lw

i.e. Area
`= l(l-6)\geq 667\\l^2-6l-667\geq 0\\(l-29)(l+23)\geq 0`

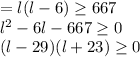
For this inequality being the product of two numbers is positive if both terms have the same sign.

This is possible only if l is atleast 29 inches (ignoring negative solution for l)

Hence possible widths are atleast 23 inches.