ANSWERS
1. Domain: all real values
2. Zeros: 0 (with multiplicity 2) and 3
3. Not periodic. Symmetric about the point (1, 2)
4. Positive for x < 3; negative for x > 3
5. f → ∞ as x → -∞; f → -∞ as x → ∞
6. none
Step-by-step explanation
1. The domain of a function is the set of all the x-values for which the function exists. In this case, we have a polynomial function and, therefore, the domain is all real values.
2. To find the zeros of the function, we have to solve,
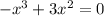
First, factor x² and -1 out. To do so, we have to divide each term by x² and by -1 - or, in other words, divide by -x²,
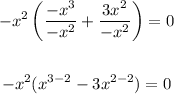
So, we have,

In this equation, we can see that if x = 0, then the equation is true. Also, if x = 3 the equation is true. So, these are the two zeros, with the particularity that x = 0 has multiplicity 2. This is because the factor related to that zero is x squared.
Hence, the zeros are 0 and 3. 0 has multiplicity 2.
3. As mentioned before, this is a polynomial function, which means that it is not a periodic function. A cubic function is an odd function, and it is symmetric about the origin. However, this function is not the parent function, x³, but it is symmetric about the point (1, 2).
4. We know that the function is zero at x = 0 and at x = 3. For x < 0, the function is positive,
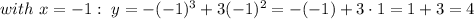
For 0 < x < 3, the function is also positive. This is because x = 0 with multiplicity 2.
Then, since the function crosses the x-axis at x = 3 and that zero has multiplicity 1, we can conclude that the function is negative for x > 3.
Hence, is the function is positive for x < 3 and negative for x > 3.
5. As mentioned in part 4, the function is positive for all values of x less than 3, which means that the function goes to infinity as x goes to negative infinity.
Since for x > 3 the function is always negative, it goes to negative infinity as x goes to infinity.
6. A polynomial function has no restrictions in the domain and, therefore, has no asymptotes.