Answer:
Tax on 2400 naira = 190 kobo
Explanation:
Given that:
The first 500 naira is tax free.
Amount earned = 2400 naira
Amount to be taxed = 2400 - 500 = 1900 naira
Payable tax = 10 kobo on every naira
1 naira = 10 kobo
1900 naira =
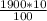
1900 naira = 190 kobo
Hence,
Tax on 2400 naira = 190 kobo