Question

Use the graph to write the explicit rule of the arithmetic sequence.

A) 
ƒ(n) = 3 + 1(n – 1)

B) 
ƒ(n) = 7 + 3(n – 1)

C) 
ƒ(n) = 7 + (–2)(n – 1)

D) 
ƒ(n) = 2 + (–7)(n – 1)

Answer 1

C

Explanation:

Answer 2

`f_n=7+\left(-2\right)\left(n-1\right)`

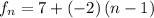
Therefore, option C is true.

Explanation:

From the graph, we get the sequence

7, 5, 3, 1, ...

Here,

a₁ = 7 is the first element.

An arithmetic sequence has a constant difference 'd' and is defined by

`f_n=a_1+\left(n-1\right)d`

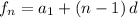
computing the differences of all the adjacent terms

`5-7=-2,\:\quad \:3-5=-2,\:\quad \:1-3=-2`

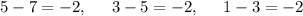
The difference between all the adjacent terms is the same and equal to

`d=-2`

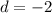
substituting a₁ = 7 and d = -2 in the nth term of the sequence

`f_n=a_1+\left(n-1\right)d`

`f_n=7+\left(-2\right)\left(n-1\right)`

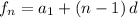
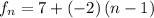
Therefore, option C is true.