Answer:
Let
 ,
,
 , and
, and
 denote three constants (with the requirement that
denote three constants (with the requirement that
 .) The following assumes that the mass of this object is
.) The following assumes that the mass of this object is
 . Assume that
. Assume that
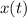 denotes the position of the object at time
denotes the position of the object at time
 .
.
(a)
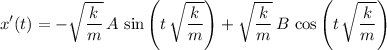 .
.
(b)

Step-by-step explanation:
The differential equation for a simple harmonic motion might take the following form:
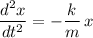 .
.
The minus sign on the right-hand side highlights the fact that the displacement and acceleration of the object should be in opposite directions.
Notice how this equation is in the form of a homogeneous second-order ODE:
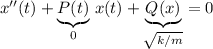
Let
 be a constant. One possible solution to this homogeneous second-order ODE would be in the form
be a constant. One possible solution to this homogeneous second-order ODE would be in the form
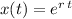 , such that
, such that
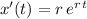 whereas
whereas
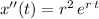 .
.
Substitute into the original ODE to obtain:
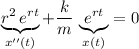 .
.
Rearrange the equation and solve for
 .
.
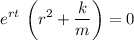
Notice that
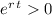 . Hence, it must be true that
. Hence, it must be true that
 . Solve for
. Solve for
 given that
given that
 :
:
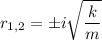 , where
, where
 is the imaginary unit.
is the imaginary unit.
The two particular solutions for the ODE would be:
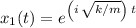 and
and
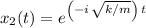 .
.
Apply Euler's Formula to rewrite both solutions in terms of trigonometric functions:
 .
.
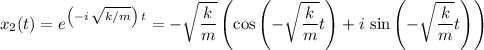 .
.
The general solution would be in the form:
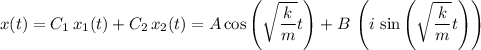 ,
,
Where
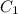 and
and
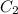 are constants (not necessarily real numbers.)
are constants (not necessarily real numbers.)
Since position is supposed to assume a real value for any real
 , set
, set
 to a multiple of
to a multiple of
 such that the general solution is real-valued:
such that the general solution is real-valued:
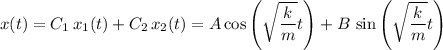 .
.
Differentiate to obtain general expressions for velocity (first derivative) and acceleration (second derivative.)