Question

(GEOMETRY PLS HELP SERIOUSLY) A treasure map says that a treasure is buried so that it partitions the distance between a rock and a tree in a 5:9 ratio. Marina traced the map onto a coordinate plane to find the exact location of the treasure.

What are the coordinates of the treasure? If necessary, round the coordinates to the nearest tenth.

A.(11.4, 14.2)

B.(7.6, 8.8)

C.(5.7, 7.5)

D.(10.2, 12.6)

Answer 1

(7.6,8.8)

Explanation:

second option

Answer 2

You have coordinates of tree T(16,21) and of rock R(3,2). Let S be a point that denotes treasure. Since treasure is buried so that it partitions the distance between a rock and a tree in a 5:9 ratio, you can state that

`\frac{\overrightarrow{RS}}{\overrightarrow{ST}}=(5)/(9).`

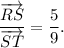
Find the coordinates of these vectors:

`\overrightarrow{RS}=(x_S-3,y_S-2), \\ \overrightarrow{ST}=(16-x_S,21-y_S).`

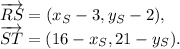
Then

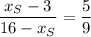`(x_S-3)/(16-x_S) =(5)/(9)` and
`(y_S-2)/(21-y_S) =(5)/(9).`

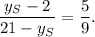
Solve these two equations:

1.

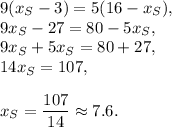
`9(x_S-3)=5(16-x_S),\\ 9x_S-27=80-5x_S,\\ 9x_S+5x_S=80+27,\\14x_S=107,\\ \\x_S=(107)/(14)\approx 7.6.`

2.

`9(y_S-2)=5(21-y_S),\\9y_S-18=105-5y_S,\\9y_S+5y_S=105+18,\\14y_S=123,\\ \\y_S=(123)/(14)\approx 8.8.`

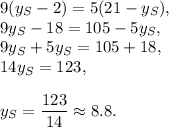
Answer: the treasure are placed at point (7.6,8.8), so the correct choice is B.