Answer:
The amount of solid ice remaining after 6 hours is approximately 3.68664 kg
Step-by-step explanation:
The given parameters are;
The side length of the cube box, s = 3(0) cm = 0.3 m
The thickness of the cube box, d = 5.0 cm = 0.05 m
The mass of ice in the box, m = 4.0 kg
The outside temperature of the cube box, T₁ = 45°C
The temperature of the melting ice inside the box, T₂ = 0°C
The latent heat of fusion of ice,
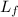 = 3.35 × 10⁵ J/K/hr/kg
= 3.35 × 10⁵ J/K/hr/kg
The surface area of the box, A = 6·s² 6 × (0.3 m)² = 0.54 m²
The coefficient of thermal conductivity, K = 0.01 J/s·m⁻¹·K⁻¹
For thermal equilibrium, we have;
The heat supplied by the surrounding = The heat gained by the ice
The heat supplied by the surrounding, Q = K·A·ΔT·t/d
Where;
ΔT = T₁ - T₂ = 45° C - 0° C = 45° C
ΔT = 45° C
Q = K·A·ΔT·t/d = 0.01 × 0.54 × 45 × 6× 60×60/0.05 = 104976
∴ The heat supplied by the surrounding, Q = 104976 J
The heat gained by the ice =
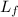 ×
×
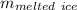 =3.35 × 10⁵ J/kg ×
=3.35 × 10⁵ J/kg ×
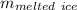
Therefore, from Q =
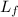 ×
×
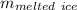 , we have;
, we have;
Q = 104976 J =
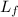 ×
×
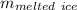 = 3.35 × 10⁵ J/kg ×
= 3.35 × 10⁵ J/kg ×
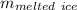
104976 J = 3.35 × 10⁵ J/kg ×
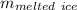
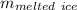 = 104976 J/(3.35 × 10⁵ J/kg) ≈ 0.31336 kg
= 104976 J/(3.35 × 10⁵ J/kg) ≈ 0.31336 kg
The mass of melted ice,
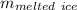 ≈ 0.31336 kg
≈ 0.31336 kg
∴ The amount of solid ice remaining after 6 hours,
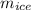 = m -
= m -
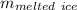
Which gives;
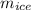 = m -
= m -
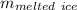 = 4.0 kg - 0.31336 kg ≈ 3.68664 kg
= 4.0 kg - 0.31336 kg ≈ 3.68664 kg
The amount of solid ice remaining after 6 hours,
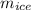 ≈ 3.68664 kg.
≈ 3.68664 kg.