Question

George is trying to create a rectangular box with a square base to ship his product in. he wants it to enclose the maximum volume but he only has 56 square feet of material to use. in order to find the dimensions he sets up two equations:

Answer 1

Length and width of the box = 3.05 feet

Height of the box = 6.12 feet

Explanation:

Let the side of square base of the rectangular box is x feet and height is h feet.

therefore volume of the box V = x² × h-----------(1)

It has been given that George has a material to create the box with an area = 56 square feet

Box consists one base + one cover + four sides

So area of a rectangular box with square base = 2×(area of base) + 4×(area of one side) = 56 square feet

2(x)²+ 4(xh) = 56

2(x² + 2xh) = 56

x² + xh = 28

xh = 28 - x²

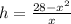`h=(28-x^(2) )/(x)`-------(2)

Now we put the value of h in equation (1)

`V=[(28-x^(2))/(x)]x^(2)=x(28-x^(2))`

To find the maximum volume we will find the derivative of volume and then equate it to zero.

V=28x - x³

`(dV)/(dx)=28-3x^(2)=0`

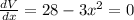
3x² = 28

`x=\sqrt{(28)/(3) } =√(9.33)=3.05`

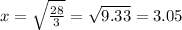
Now we put the value of x in equation 2

`h=(28-(3.05)^(2))/(3.05)=(28-9.33)/(3.05)=6.12feet`

Therefore length and width of the box are 3.05 feet and height is 6.12 feet

Answer 2

to solve the problem we must set the equation for the volume and surface area
let x be the side of the square base
and h be the height of the box

so the volume , v = hx^2
and the area, a = x^2 + xh = 56
then solve for the equation of h
x^2 + xh = 56
xh = 56 - x^2
h = 56/x - x

to solve the maximum volume, solve the first derivative of the volume and equate to zero

v = hx^2
v = (56/x - x) x^2
v = 56x - x^3
dv/dx = 56 - 3x^2
0 = 56 - 3x^2
3x^2 = 56
x = 4.32 ft
h = 8.64 ft