Answer:
The required order of polynomial is
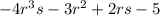 .
.
Explanation:
The given polynomial is

We have to arrange the polynomial in descending powers of r.
In term 2rs, the power of r is 1.
In term -5, the power of r is 0.
In term -3r², the power of r is 2.
In term -4r³s, the power of r is 3.
On arranging the polynomial in descending powers of r, we get
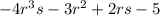
Therefore the required order of polynomial is
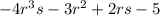 .
.