Each sector is formed like a triangle with a circle base. The sum of all the bases should be equal to half the length of the circle's circumference, this is calculated with the following expression:
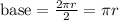
This is the base of the parallelogram.
The height of each triangle is the radius of the circle, therefore:
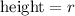
The area of the parallelogram is the product of the base and the height.

So the base is pi*r;
The height is r;
The area is pi*r².