Question

Yvonne wants to use a dissection argument to justify the formula for the area of a circle. She dissects the circle into congruent sectors and reassembles the sectors as a parallelogram-like figure. The diagram below shows the arrangement for a circle dissected into 8 sectors. M Height Base Yvonne knows that as the number of sectors of the circle increases, the reassembled figure becomes closer and closer to an actual parallelogram so that it can be used to determine the area of the circle. Determine the value of each characteristic of the parallelogram in the table below. Select the best value for each characteristic.base of the parallelogram height of the parallelogram area of the parallelogram

Answer 1

Each sector is formed like a triangle with a circle base. The sum of all the bases should be equal to half the length of the circle's circumference, this is calculated with the following expression:

`\text{base}=(2\pi r)/(2)=\pi r`

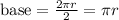
This is the base of the parallelogram.

The height of each triangle is the radius of the circle, therefore:

`\text{height}=r`

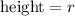
The area of the parallelogram is the product of the base and the height.

`\text{Area =}\pi r^2`

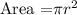
So the base is pi*r;

The height is r;

The area is pi*r².