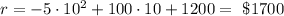Question

Mr. Stern owns an apartment building with 60 suites. He can rent all the suites if he charges a monthly rent of $200 per suite. At a higher rent, some suites will remain vacant. On the average, for each increase of $5, one suite remains vacant with no possibility of renting it. Determine the functional relationship between the total monthly revenue and the number of vacant units. What monthly rent will maximize the total revenue? What is the monthly revenue?

Answer 1

If Mr. Stern charges a monthly rent of $200, we still can rent all suites. An average increase of $5 in the monthly rent imply in the addition of one suite vacant.

Therefore, the total monthly revenue r in function of the number of vacant units v can be writen in the form:

`\begin{gathered} r=(200+5v)\cdot(60-v) \\ r=-5v^2+100v+1200 \\ 0\leq v\leq60 \end{gathered}`

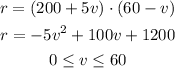
The monthly rent m is given by:

`m=200+5v`

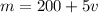
The value of v that maximize the total revenue r is the one found in the vertex of the parabola that represents r:

`v_(\max )=-(100)/(2\cdot(-5))=10`

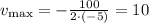
Therefore, the monthly rent that maximize the total revenue is m = 200 + 5*10 = $700

The monthly revenue with this monthly rent is:

`r=-5\cdot10^2+100\cdot10+1200=\text{ \$1700}`