Question

State the number of complex zeros and the possible number of real and imaginary zeros for each function. Then find all zeros. show all work

Answer 1

We have a cubic function

`f(x)=x^3-3x^2-47x-87`

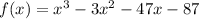
One way to find all the zeros is by factoring, we can easily find the first zero using the divisors test if we have an independent term, at our case it's -87, one of the divisors may be a zero. The divisors of -87 is 1, 3, 29 and 87.

If we check for all of the divisors we will see that -3 is a zero. (Check with both signals).

If -3 is a zero, the D'Alembert theorem tells us that f(x) is divisible by (x+3), if we do that division we'll have a quadratic function where we can just apply the quadratic formula, then

There's a theorem that says that, if f(a) is a zero, i.e f(a) = 0, and f(x) is a polynomial, then f(x) is divisible by (x-a), in other words, we can divide f(x) by (x-a) and the rest of the division will be 0.

Therefore, let's divide our function by (x+3)

Then we can write our function as

`f(x)=(x+3)(x^2-6x-29)`

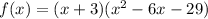
Look that now we have a quadratic function, and we can easily find its zeros, applying the quadratic formula

`x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}`

We have a = 1, b = -6 and c = -29. Then

`\begin{gathered} x=\frac{6\pm\sqrt[]{36+4\cdot29}}{2} \\ \\ x=\frac{6\pm\sqrt[]{156}}{2} \\ \\ x=\frac{6\pm2\sqrt[]{38}}{2} \\ \\ x=3\pm\sqrt[]{38} \end{gathered}`

Now we have all the zeros of f(x), it's

`\begin{gathered} x=-3 \\ \\ x=3+\sqrt[]{38} \\ \\ x=3-\sqrt[]{38} \end{gathered}`

As we can see there's no complex zero, all the zeros are real numbers.

The max number of complex zeros is 2 because the complex zeros always come in pairs, so if we have 1 complex zero, automatically we have another, for a 3-degree equation, there's a maximum of 2 complex zeros and 1 real zero, or all the of them are real.

Then the correct answer is A)