Question

If W, V, and U are the midpoints of triangle SRT, find SR.

A.
1.7
B.
2.3
C.
3.4
D.
4.6

Answer 1

The answer is either B or D

Answer 2

4.6

Explanation:

W is the mid point of ST

U is the mid point of SR

V is the mid point of TR

Mid point theorem : It states that the segment joining two sides of a triangle at the midpoints of those sides is parallel to the third side and is half the length of the third side.

So By theorem,
`(TR)/(2)=WU`

WU = 1.7

So,
`(TR)/(2)=1.7`

`RT=1.7 * 2`

`RT=3.4`

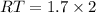
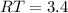
Since V is the midpoint of RT

So,
`TV=RV=(RT)/(2)`

`TV=RV=(3.4)/(2)=1.7`

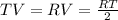
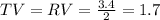
Basic Proportionality Theorem : It states that, if a line is parallel to a side of a triangle which intersects the other sides into two distinct points, then the line divides those sides in proportion.

So, Using theorem :

`(RV)/(RT)=(UR)/(SR)`

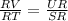
So,
`(1.7)/(3.4)=(2.3)/(SR)`

`SR=2.3* (3.4)/(1.7)`

`SR=4.6`

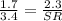
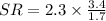
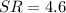
Thus the length of SR is 4.6

Hence Option D is true.