Answer : The mechanical energy of the rock is, 134 J
Solution :
As we know that the mechanical energy is equal to the sum of the kinetic energy and the potential energy.
The formula used for mechanical energy is,
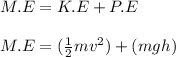
where,
M.E = mechanical energy
K.E = kinetic energy
P.E = potential energy
m = mass of an object = 2 Kg
v = velocity of an object = 6 m/s
h = height = 5 m
g = acceleration due to gravity =
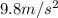
Now put all the given values in the above formula, we get the mechanical energy of the rock.
![M.E=[(1)/(2)(2Kg)* (6m/s)^2]+(2Kg* 9.8m/s^2* 5m)=134\text{ Kg }m^2s^(-2)=134J](https://img.qammunity.org/2018/formulas/physics/high-school/o6kjsl9u6ku1fuhor3sbizx5eb6m75hqev.png)
Therefore, the mechanical energy of the rock is, 134 J