Question

Find the series:0,2,6,12,20and.......?​

Answer 1

The series is represented by sum
`f(n) = 2 \cdot \Sigma\limits_(i=0)^(n) n`,
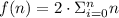`n \in\mathbb{N }`. The remaining element of the series is 30.

Explanation:

This exercise consist in deriving the function which contains every element of the given series. The sum that contains all elements of the series { 0, 2, 6, 12, 20,...} is represented by the following formula:

`f(n) = 2 \cdot \Sigma\limits_(i=0)^(n) n`,
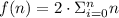`n \in\mathbb{N }` (1)

Where
`n` is the cardinal associated with the element of the series.

Lastly, we proceed to evaluate the sum for the first five elements:

n = 0

`f(0) = 0`

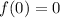
n = 1

`f(1) = 0 +2`

`f(1) = 2`

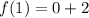
n = 2

`f(2) = 0 + 2 + 4`

`f(2) = 6`

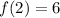
n = 3

`f(3) = 0 + 2 + 4 + 6`

`f(3) = 12`

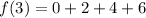
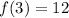
n = 4

`f(4) = 0+2+4+6+8`

`f(4) = 20`

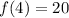
The series is represented by sum
`f(n) = 2 \cdot \Sigma\limits_(i=0)^(n) n`,
`n \in\mathbb{N }`.

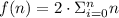Lastly, the missing element is found by evaluating the function at
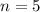`n = 5`, that is:

n = 5

`f(5) = 0 + 2 + 4 + 6 + 8 + 10`

`f(5) = 30`

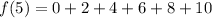
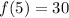
The remaining element of the series is 30.