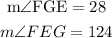Question

The circle below has center E. Suppose that m

Answer 1

Notice that the triangle △GEF is an isosceles triangle, since GE=EF (both sides are radii of the circle).

Since △GEF is an isosceles triangle with GE=EF, then the measure of the angles opposed to those sides is the same:

`m\angle GFE=m\angle EGF`

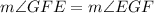
Since the line FH is tangent to the circle, the angle ∠HFE is a right angle.

Since ∠HFG and ∠GFE are adjacent angles, then:

`m\angle\text{HFG}+m\angle\text{GFE}=m\angle\text{HFE}`

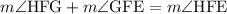
Substitute m∠HFG=62 and m∠HFE=90 to find m∠GFE:

`\begin{gathered} 62+m\angle\text{GFE}=90 \\ \Rightarrow m\angle GFE=28 \end{gathered}`

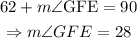
Since the sum of the internal angles of any triangle is 180 degrees, then:

`m\angle\text{GFE}+m\angle\text{EGF}+m\angle\text{FEG}=180`

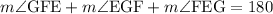
Substitute the values of m∠GFE and m∠EGF:

`\begin{gathered} 28+28+m\angle\text{FEG}=180 \\ \Rightarrow\angle FEG=124 \end{gathered}`

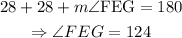
Therefore:

`\begin{gathered} \text{m}\angle\text{FGE}=28 \\ m\angle FEG=124 \end{gathered}`