Question

The separation distance between two 2.0 kg masses is decreased by two-thirds. How is the gravitational force between them affected?

Answer 1

Given:

The mass of two objects is: m1 = m2 = m = 2 kg

The distance between the object is decreased by two-thirds

To find:

How on reducing the distance, the gravitational force between them affects them.

Step-by-step explanation:

Let the distance between two objects each having mass "m" be "r". The gravitational force between them is given as:

`F_1=G(m_1* m_2)/(r^2)`

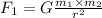
Here, G is the universal gravitational constant.

Substituting the values in the above equation, we get:

`\begin{gathered} F_1=G*\frac{2\text{ kg}*2\text{ kg}}{r^2} \\ \\ F_1=G*\frac{4\text{ kg}^2}{r^2}..........(1) \end{gathered}`

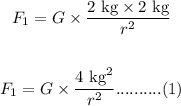
Now, the distance between the mass is reduced by two-thirds. Thus, the new distance between them will be "R" which is given as:

`R=r-(2)/(3)r=r(1-(2)/(3))=(r)/(3)`

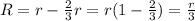
Now, the gravitational force between two masses with their distance of separation reduced by two-thirds is given as:

`F_2=G(m_1* m_2)/(R^2)`

Substituting the values in the above equation, we get:

`\begin{gathered} F_2=G*\frac{2\text{ kg}*2\text{ kg}}{((r)/(3))^2} \\ \\ F_2=G*\frac{4\text{ kg}^2}{(r^2)/(9)} \\ \\ \begin{equation*} F_2=G*\frac{9*4\text{ kg}^2}{r^2} \end{equation*} \\ \\ F_2=9*(G*\frac{4\text{ kg}^2}{r^2})..........(2) \end{gathered}`

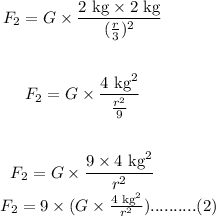
Substituting equation (1) in equation (2), we get:

`\begin{gathered} F_2=9*(G*\frac{4\text{ kg}^2}{r^2}) \\ \\ F_2=9F_1 \end{gathered}`

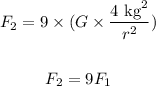
From the above equation, we observe that the new gravitational force F2 between two masses when their distance of separation is reduced by two-thirds will be nine times that of the original value of gravitational force F1.

Final answer:

The new gravitational force F2 between two masses when their distance of separation is reduced by two-thirds will be nine times that of the original value of gravitational force F1.