Answer:
The orbital radius is approximately 42,259 kilometers.
Step-by-step explanation:
From Newton's Law of Gravitation we find that acceleration experimented by the satellite (
 ), measured in meters per square second, is defined by:
), measured in meters per square second, is defined by:
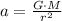 (1)
(1)
Where:
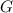 - Gravitational constant, measured in cubic meters per kilogram-square second.
- Gravitational constant, measured in cubic meters per kilogram-square second.
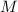 - Mass of Earth, measured in kilograms.
- Mass of Earth, measured in kilograms.
 - Orbital radius, measured in meters.
- Orbital radius, measured in meters.
By supposing the satellite rotates at constant speed and in a circular path, we find that acceleration is entirely centripetal and can be defined in terms of period, that is:
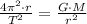
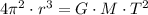

![r = \sqrt[3]{(G\cdot M\cdot T^(2))/(4\pi^(2)) }](https://img.qammunity.org/2022/formulas/physics/high-school/uhv9x22gzhqvrt9zclvg8ehfawfgniz4qa.png)
Where
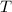 is period, measured in seconds.
is period, measured in seconds.
If we know that
 ,
,
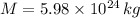 and
and
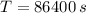 , then orbital radius of the satellite is:
, then orbital radius of the satellite is:
![r = \sqrt[3]{(\left(6.674\cdot 10^(-11)\,(m^(2))/(kg\cdot s^(2)) \right)\cdot (5.98* 10^(24)\,kg)\cdot (86400\,s)^(2))/(4\pi^(2)) }](https://img.qammunity.org/2022/formulas/physics/high-school/5br18lu5vuqkqsk2imk8zjo3vblsed5scu.png)
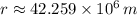

The orbital radius is approximately 42,259 kilometers.