Question

Which graph represents the solution set for the quadratic inequality x2 + 2x + 1 > 0?

Answer 1

Answer: C

Explanation:

Answer 2

We have to determine the graph of the given inequality as:

`x^2+2x+1>0`

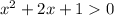
on solving this equation we get:

`(x+1)^2>0`

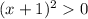
Since we know that:

`(x+1)^2=x^2+1^2+2* x* 1\\\\(x+1)^2=x^2+1+2x`

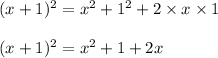
Now we know that when
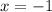`x=-1` the value of:

`(x+1)^2=0`

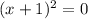
Also for the value other than -1 the function being a quadratic function will always give a non-zero positive value.

Hence, range of the function in intervals could be written as:

(-∞,-1)∪(-1,∞).

Hence, the graph of the function will be the whole of the number line with a open circle on -1.