Answer:
We have to determine the graph of the given inequality as:
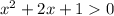
on solving this equation we get:

Since we know that:
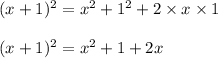
Now we know that when
 the value of:
the value of:
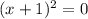
Also for the value other than -1 the function being a quadratic function will always give a non-zero positive value.
Hence, range of the function in intervals could be written as:
(-∞,-1)∪(-1,∞).
Hence, the graph of the function will be the whole of the number line with a open circle on -1.