Question

Suppose a ball is dropped from a height of 16 feet. Each time it drops h feet, it rebounds 0.81h feet. Find the total distance traveled by the ball. Round your answer to two decimal places

Answer 1

When the ball is first dropped, it falls
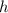
`h` feet. On the first bounce, it rebounds
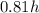
`0.81h` feet, which means on the second "drop" it must travel
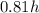
`0.81h` feet again. On the second bounce, the ball rebounds
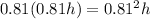
`0.81(0.81h)=0.81^2h` feet, and on the third drop falls the same distance. And so on.

So there are two directions to track:


`\text{downward: }\displaystyle h+0.81h+0.81^2h+\cdots=\sum_(n=0)^\infty 0.81^nh`

`\text{upward: }\displaystyle 0.81h+0.81^2h+\cdots=\sum_(n=1)^\infty 0.81^nh`

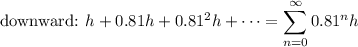
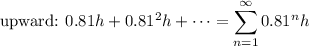
The total distance is the sum of these two:


`\displaystyle\sum_(n=0)^\infty 0.81^nh+\sum_(n=1)^\infty 0.81^nh=h+2h\sum_(n=1)^\infty 0.81^n`

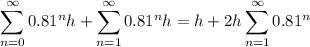
Recall that for an infinite geometric sum, you have


`\displaystyle\sum_(n=0)^\infty r^n=1+\sum_(n=1)^\infty r^n=\frac1{1-r}`

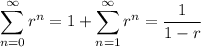
provided that
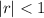
`|r|<1`. So the total distance traveled by the ball is


`h+2h\left(\frac1{1-0.81}-1\right)\approx9.53h`

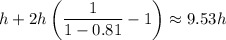
Starting with a height of
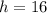
`h=16` means the total distance is about 152.42 ft.