Question

When comparing mass and size data for the planets Earth and Jupiter, it is observed that Jupiter is about 300 times more massive than Earth. One might quickly conclude that an object on the surface of Jupiter would weigh 300 times more than on the surface of the Earth. For instance, one might expect a person who weighs 500 N on Earth would weigh 150000 N on the surface of Jupiter. Yet this is not the case. In fact, a 500 N person on Earth weighs about 1500 N on the surface of Jupiter. Explain how this can be.

Answer 1

This situation happens because radius of Jupiter is 10 times greater than radius of the Earth.

Step-by-step explanation:

According to Newton's Law of Gravitation, weight is directly proportional to the mass of the planet (
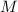`M`), measured in kilograms, and inversely proportional to the square of the radius of the planet (
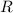`R`), measured in meters. That is:

`W \propto (M)/(R^(2))`

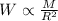
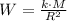`W = (k\cdot M)/(R^(2))`(1)

Where
`k` is proportionality constant, measured in Newton-square meters per kilogram.

Then, we eliminate the proportionality constant by constructing this relationship:

`(W_(J))/(W_(E)) = \left((M_(J))/(M_(E))\right)\cdot \left((R_(E))/(R_(J)) \right)^(2)`

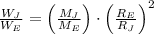
Where subindices J and E mean "Jupiter" and "Earth", respectively. If we know that
`(M_(J))/(M_(E)) = 300`,
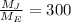`W_(E) = 500\,N`and
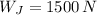`W_(J) = 1500\,N`, then the ratio of radii is:

`(R_(E))/(R_(J)) = \sqrt{\left((W_(J))/(W_(E)) \right)\cdot \left((M_(E))/(M_(J)) \right)}`

`(R_(E))/(R_(J)) = \sqrt{3\cdot \left((1)/(300) \right)}`

`(R_(E))/(R_(J)) = (1)/(10)`

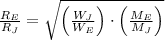
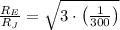
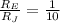
Therefore, this situation happens because radius of Jupiter is 10 times greater than radius of the Earth.