Question

I need help solving the equal method

Answer 1

(-2, -4)

Explanation:

Since both equations are equal to y, you can set them equal to each other:

`(3)/(2)x-1=(1)/(2)x-3`

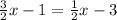
Next, solve for x:

`(3)/(2)x-1=(1)/(2)x-3\\x-1=-3\\x=-2`

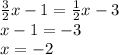
Finally, substitute the solution for x in one of the equations (or both) to find y:

`y=(3)/(2)(-2)-1\\y=-3-1\\y=-4`

`y=(1)/(2)(-2)-3\\y=-1-3\\y=-4`

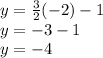
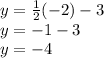
Therefore, the solution to the system of equations is (-2, -4).