Question

6. m A = 8x - 2, m B = 2x - 8, and m2 C = 94 - 4x. List the sides of A ABC in order from shortest to

longest.
AC: AB: BC
AC :BC: AB
AB: AC : BC
BC: AC : AB

Answer 1

Given:

In triangle ABC, m∠A=(8x-2)°, m∠B=(2x-8)° and m∠C=(94-4x)°.

To find:

The sides of the triangle ABC in order from shortest to longest.

Solution:

In triangle ABC,

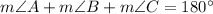`m\angle A+m\angle B+m\angle C=180^\circ` (Angle sum property)

`(8x-2)^\circ+(2x-8)^\circ+(94-4x)^\circ=180^\circ`

`(6x+84)^\circ=180^\circ`

`6x+84=180`

`6x=180-84`

`6x=96`

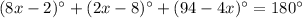
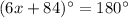
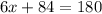
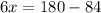
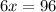
Divide both sides by 6.

`x=(96)/(6)`

`x=16`

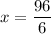
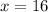
Now,

`m\angle A=(8(16)-2)^\circ`

`m\angle A=(128-2)^\circ`

`m\angle A=126^\circ`

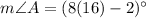
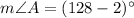
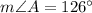
Similarly,

`m\angle B=(2(16)-8)^\circ`

`m\angle B=(32-8)^\circ`

`m\angle B=24^\circ`

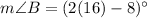
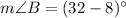
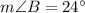
And,

`m\angle C=(94-4(16))^\circ`

`m\angle C=(94-64)^\circ`

`m\angle C=30^\circ`

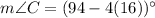
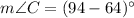
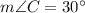
In a triangle the smaller angle has shorter opposite side and larger angle has longer opposite side.

`24^\circ<30^\circ<126^\circ`

`m\angle B<m\angle C<m\angle A`

`AC<AB<BC`

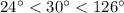
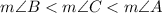
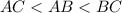
List the sides of triangle ABC in order from shortest to longest is AC:AB:BC.

Therefore, the correct option is A.