Answer: The correct option is the second one, counting from the top.
Explanation:
For a rectangle of length L, and width W, the area can be calculated as:
A = L*W
In this case, we know that:
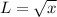
and
![W = \sqrt[3]{x^2}](https://img.qammunity.org/2022/formulas/mathematics/college/4klgkordns7762sn95ssomh010ouwg4cpx.png)
First, we need to remember the relations;
![\sqrt[n]{x^m} = x^(m/n)](https://img.qammunity.org/2022/formulas/mathematics/college/b8011p9bqdzshce76cmzoo8lvcn9nszt75.png)
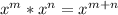
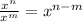
a) Now we can calculate the area of the rectangle as:
![A = L*W = √(x) *\sqrt[3]{x^2} = (x^(1/2))*(x^(2/3)) = x^(1/2 + 2/3) = x^(3/6 + 4/6) = x^(1/6 + 1)](https://img.qammunity.org/2022/formulas/mathematics/college/2ba4gke57hvyxurs00trgntnk7nx286d9n.png)
And we can write that last part as:
![x^(1/6 + 1) = x*x^(1/6) = x*\sqrt[6]{x}](https://img.qammunity.org/2022/formulas/mathematics/college/4ieop3cj76q6ucgrik3kv8xbmc798sdoj8.png)
b) Now we want to find the ratio between the width and the length:
![(W)/(L) = \frac{\sqrt[3]{x^2} }{√(x) } = (x^(2/3))/(x^(1/2)) = x^(2/3 - 1/2) = x^(4/6 - 3/6) = x^(1/6) = \sqrt[6]{x}](https://img.qammunity.org/2022/formulas/mathematics/college/8l3s8f23l9rua5f8q8hlhpwu7upreyixek.png)
Now, if x = 1, the ratio will be equal to 1.
if x > 1, the ratio will be larger than 1.
if 0 < x < 1, the ratio will be smaller than 1.
The correct option is the second one, counting from the top.