Question

Factor completely: 3a2 − 14a − 24

(3a − 4)(a + 6)
(3a + 4)(a − 6)
(3a − 6)(a + 4)
Prime

Answer 1

i know what it is. it  is (3a+4)(a-6)

Answer 2

The correct option is (3a+4)(a-6)

Explanation:

We have the polynomial
`3a^2-14a-24`

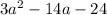
For the polynomials of the form
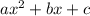`ax^2+bx+c` we have to rewrite the middle term as a sum of two terms whose product is, in this case, a.c=-72 and whose sum is b=(-14)

We have to factorize -14 from -14a:

`3a^2-14(a)-24=\\3a^2-(18-4)(a)-24=\\=3a^2-18a+4a-24`

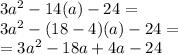
Because b=(-18)+4=(-14) and a.c=(-18).4=(-72)

Now we have to factor by grouping:

`3a^2-18a+4a-24=\\(3a^2-18a)+(4a-24)=\\3a(a-6)+4(a-6)=\\=(3a+4)(a-6)`

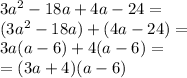
Then, the correct option is (3a+4)(a-6)