Question

What is the pi times the definite integral from 0 to pi of sin(sin(x)^2 dx

Answer 1

Since
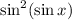
`\sin^2(\sin x)` doesn't have an elementary antiderivative, it's unlikely that there is an exact answer here. However, there are some facts you can use to make a good approximate guess.

One thing you can do is approximate the function by


`y\approx\begin{cases}\frac{2\sin1}\pi x&\text{for }0\le x<\frac\pi2\\\\2\sin1\left(1-\frac1\pi x\right)&\text{for }\frac\pi2\le x<\pi\end{cases}`

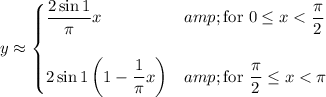
Then the volume is approximately


`\pi\left(\int_0^(\pi/2)\left(\frac{2\sin1}\pi x\right)^2\,\mathrm dx+\int_(\pi/2)^\pi\left(2\sin1\left(1-\frac1\pi x\right)\right)^2\,\mathrm dx\right)`

which evaluates to
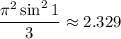
`\frac{\pi^2\sin^21}3\approx2.329`. The actual volume is slightly larger, since
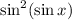
`\sin^2(\sin x)` is slightly greater than this approximating function. The closest answer is 3.830. Indeed, the actual value to 20 decimal places is about 3.8299454909568467491, so this is the correct answer.

Note that a better approximating function would yield a better solution. If you know about Taylor series, you can use that to your advantage and approximate
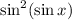
`\sin^2(\sin x)` with, say, a 4th degree polynomial that would be easy to integrate and yield a result much closer to the actual value.