Question

M(9, 8) is the midpoint of RS . The coordinates of S are (10, 10). What are the coordinates of R?

A) (18, 16)

B) (11, 12)

C) (9.5, 9)

D) (8, 6)

Answer 1

Answer: D) (8, 6)

Explanation:

If (x,y) is a midpoint of a line segment joining
`(x_1,y_1)` and
`(x_2,y_2)` such that

`x=(x_1+x_2)/(2)` and
`y=(y_1+y_2)/(2)` (1)

Given : M(9, 8) is the midpoint of RS . The coordinates of S are (10, 10).

Let The coordinate of point R be (a,b).

Using (1) , we have

`9=(a+10)/(2)` and
`8=(b+10)/(2)`

`\Rightarrow\ 2(9)=a+10`and
`2(8)=b+10`

`\Rightarrow\ 18=a+10`and
`16=b+10`

`\Rightarrow\ a=18-10=8`and
`b=16-10=6`

i.e. (a,b) = (8, 6)

Hence, the coordinates of R = (8, 6)

Thus , the correct answer is D) (8, 6)

Answer 2

D) (8, 6)

Explanation:

Given: M(9, 8) is the midpoint of RS . The coordinates of S are (10, 10).

Here we have to use the mid-point formula:

`x = (x_1 + x_2)/(2)  ; y = (y_1 + y_2)/(2)`

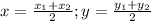
Here (x, y) is the midpoint.

(x, y) = M(9, 8)

(x2, y2) = (10, 10)

Here x = 9, y = 8 and x2 = 10 and y2 = 10

Now let's plug in these values in the mid-point formula and find (x1, y1)

`9 = (x_1 + 10)/(2) ; 8 = (y_1 + 10)/(2)`

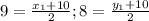
Let's simplify and find the value of x1 and y1

`18 = x_1 + 10 ; 16 = y_1 + 10\\`

`x_1 = 18 -10 ; y_1 = 16 -10`

`x_1 = 8 ; y_1 = 6`

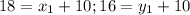
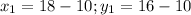
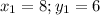
So the coordinates of R(8, 6)