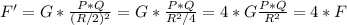Question

Fill in the chart with the correct values of F for each change in the system described in questions

Answer 1

We know that the gravitational force F between two masses P and Q, that are separated by a distance R is:

`F = G*(P*Q)/(R^2)`

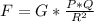
Where G is the gravitational constant.

a) Mass P is doubled, then we have 2*P instead of P, the new force is:

`F' = G*((2*P)*Q)/(R^2) = 2*(G*(P*Q)/(R^2) ) = 2*F`

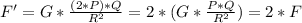
b) Now R is doubled, then instead of R, we have 2*R:

`F' = G*(P*Q)/((2*R)^2) = G*(P*Q)/(4*R^2) = G*(P*Q)/(R^2)*(1/4) = F/4`

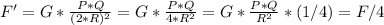
c) Now we replace P by 2*P, and Q by 3*Q

`F' = G*((2*P)*(3*Q))/(R^2) = 2*3*(G*(P*Q)/(R^2) ) = 6*F`

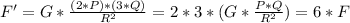
d) The entire mass of the system is increased by a factor of 4, then both of the individual masses are increased by a factor of 4.

Then we need to replace P by 4*P, and Q by 4*Q.

`F' = G*((4*P)*(4*Q))/(R^2) = 4*4(G*(P*Q)/(R^2) ) = 16*F`

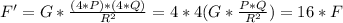
e) Now we replace R by R/2.

`F' = G*(P*Q)/((R/2)^2) = G*(P*Q)/(R^2/4)= 4*G(P*Q)/(R^2) = 4*F`