Recall the half angle identities for sine and cosine:
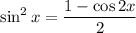
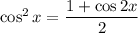
So you have
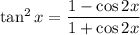
This is useful because we have
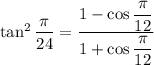
Unfortunately, we need to know the value of
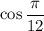
to continue. But we can use either of the half-angle identities to figure this out.
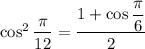
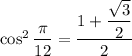
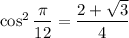
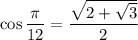
where you take the positive root since
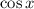
is positive when
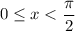
.
So, you have
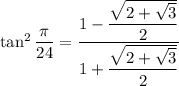
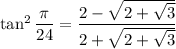
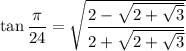
again taking the positive root because
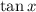
is positive when
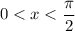
.