Question

What are the roots of x in -10x2 + 12x − 9 = 0

Answer 1

a = -10 b = 12 c = -9

x = [-12 +- sq root (144 - 4*-10*-9)] / -20

x = [-12 +- sq root (144 -360)] / -20

x1 = 3/5 + (14.7 i / -20)

x2 = 3/5 - (14.7 i / -20)

Answer 2

`x =(-12+i√(216))/(-20),(12+i√(216))/(20)`

Explanation:

Given :
`-10x^2 + 12x -9 = 0`

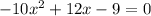
To Find: What are the roots of x?

Solution:

`-10x^2 + 12x -9 = 0`

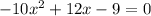
We will solve this by quadratic formula :

Formula :
`x =(-b\pm√(b^2-4ac))/(2a)`

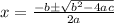
General form of quadratic equation:
`ax^2+bx+c=0`

On Comparing the given equation with general form.

a = -10

b= 12

c = -9

Substitute the values in the formula :

`x =(-b\pm√(b^2-4ac))/(2a)`

`x =(-12\pm√(12^2-4(-10)(-9)))/(2(-10))`

`x =(-12\pm√(-216))/(-20)`

`x =(-12+√(-216))/(-20),(-12-√(-216))/(-20)`

`x =(-12+i√(216))/(-20),(-12-i√(216))/(-20)`

`x =(-12+i√(216))/(-20),(12+i√(216))/(20)`

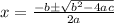
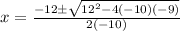
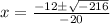
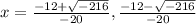
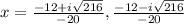
Hence the roots of x are
`x =(-12+i√(216))/(-20),(12+i√(216))/(20)`