Question

What are the potential solutions of ln(x^2 -25)= 0

Answer 1

The potential solutions are x = √26 and x = -√26

Explanation:

The given expression is ln(x² - 25) = 0

It can be rewritten as

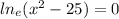`ln_(e)(x^(2)-25)=0` [Since base of a natural logarithm is considered as e]

`e^(0)=(x^(2)-25)`

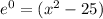
Since in a logarithmic function if
`ln_(e)b=c`

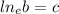
Then
`e^(c)=b`

Now we further solve the expression to get the possible roots.

`x^(2)-25=1`

`x^(2)=25+1`

`x^(2)=26`

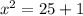
x = ±√26

Therefore, the potential solutions are x = √26 and x = -√26.

Answer 2

`\large\boxed{x=-√(26)\ \vee\ x=√(26)}`

Explanation:

`\log_ab=c\iff a^c=b,\ \text{for}\ a>0,\ a\\eq1,\ b>0\\\\\text{Domain:}\\x^2-25>0\\x^2-5^2>0\qquad\text{use}\ a^2-b^2=(a-b)(a+b)\\(x-5)(x+5)>0\to x<-5\ \vee\ x>5\\D:x\in(-\infty,\ -5)\ \cup\ (5,\ \infty)\\\\\ln(x^2-25)=0\iff x^2-25=e^0\\\\\text{we know}\ a^0=1\ \text{for all values of}\ a\ \text{except 0}\\\\x^2-25=1\qquad\text{add 25 to both sides}\\x^2=26\to x=\pm√(26)\\\\x=-√(26)\in D\\\\x=√(26)\in D`