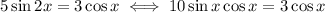
by the double angle identity for sine. Move everything to one side and factor out the cosine term.
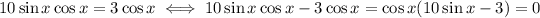
Now the zero product property tells us that there are two cases where this is true,
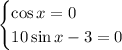
In the first equation, cosine becomes zero whenever its argument is an odd integer multiple of
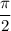
, so
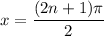
where
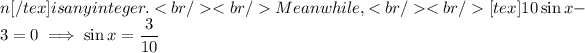
which occurs twice in the interval
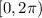
for
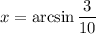
and
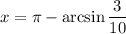
. More generally, if you think of

as a point on the unit circle, this occurs whenever

also completes a full revolution about the origin. This means for any integer

, the general solution in this case would be
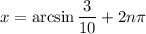
and

.