Question

For the point P(24,14) and Q(31,17), find the distance d(P,Q) and the coordinates of the midpoint M of the segment PQ.

Answer 1

STEP 1

Identify what is given and establish what is required.

We are given the coordinates of two points P and Q on the cartesian and are asked to find their midpoint M assuming a straight line is drawn from P and Q

Midpoint between two points is given as:

`\begin{gathered} M=(x_1+x_2)/(2),\text{ }\frac{y_1+y_2_{}}{2} \\ \text{Where} \\ x_1,y_{1\text{ }}are\text{ the coordinates of point 1} \\ x_2,y_{2\text{ }}are\text{ the coordinates of point }2 \end{gathered}`

STEP 2

Employ formula while putting the appropriate variables.

We select point P as our point 1 as in the formulae and

We select point Q as our point 2 as in the formulae

This gives us:

`\begin{gathered} M=(24+31)/(2),(14+17)/(2) \\ M=(55)/(2),(31)/(2) \\ M=27.5,15.5 \end{gathered}`

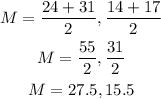
Therefore, our midpoint M is(27.5, 15.5)