STEP 1
Identify what is given and establish what is required.
We are given the coordinates of two points P and Q on the cartesian and are asked to find their midpoint M assuming a straight line is drawn from P and Q
Midpoint between two points is given as:

STEP 2
Employ formula while putting the appropriate variables.
We select point P as our point 1 as in the formulae and
We select point Q as our point 2 as in the formulae
This gives us:
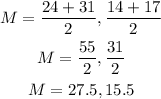
Therefore, our midpoint M is(27.5, 15.5)