Question

12% of all college students volunteer their time. Is the percentage of college students who are volunteers different for students receiving financial aid? Of the 331 randomly selected students who receive financial aid, 43 of them volunteered their time. What can be concluded at the

α
= 0.01 level of significance?

For this study, we should use
Select an answer
The null and alternative hypotheses would be:

H
0
:

?

Select an answer

(please enter a decimal)


H
1
:

?

Select an answer

(Please enter a decimal)

The test statistic
?
=
(please show your answer to 3 decimal places.)
The p-value =
(Please show your answer to 4 decimal places.)
The p-value is
?

α

Based on this, we should
Select an answer
the null hypothesis.
Thus, the final conclusion is that ...
The data suggest the populaton proportion is significantly different from 12% at
α
= 0.01, so there is sufficient evidence to conclude that the percentage of financial aid recipients who volunteer is different from 12%.
The data suggest the population proportion is not significantly different from 12% at
α
= 0.01, so there is insufficient evidence to conclude that the percentage of financial aid recipients who volunteer is different from 12%.
The data suggest the population proportion is not significantly different from 12% at
α
= 0.01, so there is sufficient evidence to conclude that the percentage of financial aid recipients who volunteer is equal to 12%.

Answer 1

Null Hypothesis:-H₀: P = 0.12

There is no difference between the percentage of volunteers selected from the college students.

Alternative Hypothesis:-H₁: P ≠ 0.12

There is a difference between the percentage of volunteers selected from the college students.

The calculated value Z = 0.5543 < 2.376 at 0.01 level of significance

The null hypothesis is accepted

There is a difference between the percentage of volunteers selected from the college students.

Explanation:

Step(i):-

Given that the Population proportion P= 12% = 0.12

Given that the 331 randomly selected students who receive financial aid, 43 of them volunteered their time.

Sample proportion

`p = (x)/(n) = (43)/(331) = 0.1299`

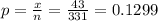
Step(ii):-

Null Hypothesis:-H₀: P = 0.12

There is a difference between the percentage of volunteers selected from the college students.

Alternative Hypothesis:-H₁: P ≠ 0.12

There is no difference between the percentage of volunteers selected from the college students.

Step(iii):-

Test statistic

`Z = \frac{p-P }{\sqrt{(PQ)/(n ) } }`

`Z = \frac{0.1299-0.12 }{\sqrt{((0.12)(0.88))/(331 ) } }`

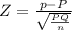
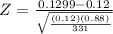
Z = 0.5543

Level of significance = 0.01

Critical value Z₀.₀₁ = 2.376

Final answer:-

The calculated value Z = 0.5543 < 2.376 at 0.01 level of significance

The null hypothesis is accepted

There is a difference between the percentage of volunteers selected from the college students.