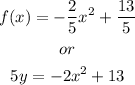Question

To the right is the graph of f(x) = x^2. The second graph, to the left of f(x) = x^2 is a new function made by stretching f(x) vertically by a factor of 2 and then translating it three units to the left and one unit down. Write the equation of the new function.

Answer 1

This problem invloves the topic of curved lines in a graph, curved lines or more speccifically curve line which looks like letter C (parabola) all follows a certain standard form of equation, which is;

`y=ax^2+b`

For example you can see that the equation for the black curve line in our picture is y=x² and notice that this equation can also be written as y = (1)x² + 0. Which simillar to the standard form given above where a is just 1 (a=1) and b is just 0 (b=0).

Since our black curve line follows the same standard form of equation as stated above, we can conclude that the RED curve line follows the same form of equation.

To summarize the steps that we must do in order to find the equation of the RED line we will list them as,

1. Sample two(2) points in the graph to be used as reference points.

2. Use the sampled points in our standar eqation in order to find the variables "a" and "b".

3. When we have the variables "a" and "b", we can just directly substitute it into our standard equation to find the equation of our RED line.

Let's start.

1. Sample 2 points to be used as refernce points. (Note that we will find the easiest points

to determine)

Let us use the points (-3, -1) and (-2, 1) as shown in the picture.

2. Use the points (-3, -1) and (-2, 1) in our standard equation.

`\begin{gathered} y=ax^2+b \\ \text{where (x,y)=(-3, -1)} \\ -1=a(-3)^2+b_{} \\ 9a+b=-1 \end{gathered}`

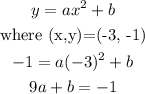
for our 1st point we have the equation 9a+b = -1, let us now proceed to our next point.

`\begin{gathered} y=ax^2+b \\ \text{where (x,y)=(-2, 1)} \\ 1=a(-2)^2+b_{}_{} \\ 1=4a+b \\ 4a+b=1 \end{gathered}`

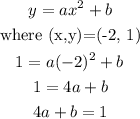
and for our 2nd point we have the equation 4a+b = 1, and by the process of subtitution and elimination we can now find "a" and "b", because we have two equations with two unknowns.

`\begin{gathered} 9a+b=-1\text{ and} \\ 4a+b=1 \end{gathered}`

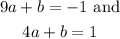
transforming eqatuin number 1 to

`9a+b=-1\text{ is just the same as b = -1 -9a}`

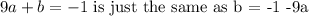
then substitue b = -1 -9a to the 2nd equation we have.

`\begin{gathered} 4a+b=1\text{ , where b = -1-9a} \\ 4a+(-1-9a)=1 \\ 4a-1-9a=1 \\ -5a=2 \\ a=-(2)/(5) \end{gathered}`

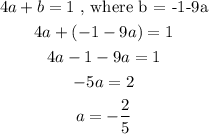
since a = -2/5, we can find b using,

`\begin{gathered} 4a+b=1\text{ , where a=-}(2)/(5) \\ 4(-(2)/(5))+b=1 \\ b=1+(8)/(5) \\ b=(5)/(5)+(8)/(5) \\ b=(13)/(5) \end{gathered}`

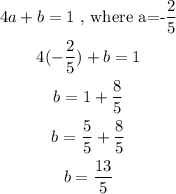
therefore our a and b are;

`a=-(2)/(5)\text{ and b = }(13)/(5)`

3. We can now proceed in substituting it in our standard equation;

`\begin{gathered} y=ax^2+b\text{ , where a = -}(2)/(5)\text{ and b = }(13)/(5) \\ y=(-(2)/(5))x^2+((13)/(5)) \\ y=-(2)/(5)x^2+(13)/(5) \end{gathered}`

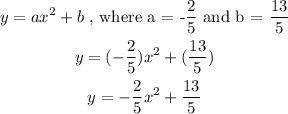
you can also simplify the final equation by multiplying all sides by 5,

`\begin{gathered} 5y=(5)\lbrack-(2)/(5)x^2+(13)/(5)\rbrack \\ 5y=-2x^2+13 \end{gathered}`

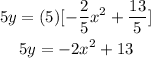
therefore our final answer can be,

`\begin{gathered} f(x)=-(2)/(5)x^2+(13)/(5) \\ or \\ 5y=-2x^2+13 \end{gathered}`