Consider the polynomial
 . You can group first two terms and second two terms:
. You can group first two terms and second two terms:
 .
.
Find the common factors in both brackets:
- in brackets
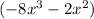 the common factor is
the common factor is
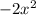 ;
; - in brackets
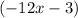 the common factor is
the common factor is
 .
.
Then rewrite the polynomial as
 .
.
Here you see that expression 4x+1 is common, then
 .
.
Answer: correct choice is D.